大学の物理化学や電気化学、生物学では『ネルンストの式』というものが登場します。この式を使えばあらゆる電池から取り出せる電位を計算することができます。
『ネルンストの式』は形こそは単純ですが、それがどのようにして導出され、どのような状況で利用でき、どのように利用するのか、など初めて学ぶ人にとっては非常に難易度が高い式です。
本記事では、ネルンストの式の導出方法や使用方法について、分かりやすく解説していきます。
>>理系課題の代行なら東大生中心スタッフ!業界最安値かつ高品質の「宿題代行Yattoku」へご依頼を
ネルンストの式とは?
ネルンストの式の概要と意味
ネルンストの式は以下のような式をしています。
$$E_{cell} = E^{o}_{cell} \,-\,\frac{RT}{νF}lnQ $$
| ・\(E_{cell}\):電池電位 (V) ・\(E^{o}_{cell}\):標準電池電位 (V) ・\(R\):気体定数 ・\(T\):絶対温度 (K) ・\(ν\):電池反応で移動する電子の量論係数 ・\(F\):ファラデー定数 ・\(Q\):電池反応の反応比 |
Cu 電極と Zn 電極を用いたダニエル電池を例に、上記ネルンストの式を解読していきます。
まず、ダニエル電池とは以下のような仕組みで動く電池です。
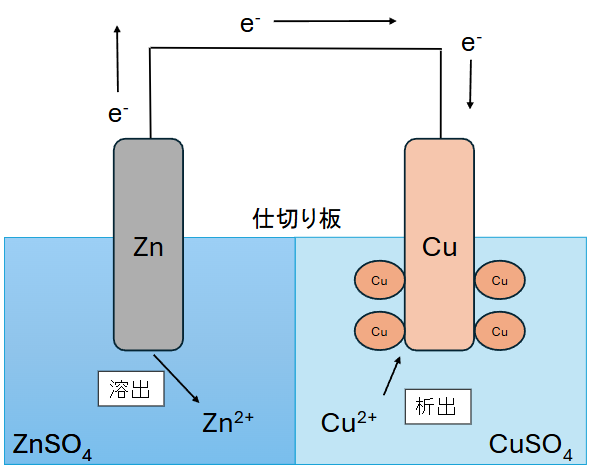
負極側では Zn 板が溶けだし、電子 e– を放出しながら Zn2+ が溶出します。正極側では Cu 板付近の Cu2+ が電子 e– を受け取り Cu が析出します。
つまり、ダニエル電池では以下のような酸化還元反応が進行することで電位を取り出すことができます。
- 負極:\( Zn → Zn^{2+} + 2e^- \)
- 正極:\(Cu^{2+} + 2e^- → Cu \)
このようなダニエル電池における反応物や生成物が標準状態(溶質や気体、固体の活量を 1、圧力 1 bar)であるときの、この電池の電圧を標準電池電位 \(E^{o}_{cell}\) といいます。すなわち、標準電池電位 (E^{o}_{cell}\) とはその電池が理想的な性能を示すときの電位というわけです。
実際には、温度などの状況によって電池電位は理想状態から離れるので、現実に取り出せる電圧を電池電位 \(E_{cell}\) といいます。すなわち、電池電位 \(E_{cell}\) が現実での電池の性能を示す値ということです。
また、負極と正極の上記酸化還元反応では電子 e– が2つ移動していると思います。電子 e– が一度の反応で何個移動しているか、これを電池反応で移動する電子の量論係数 \(ν\) として表現しています。
電池反応の反応比 \(Q\) とは、その電池反応でどの程度反応が起きるかという指標であり、酸化反応(Oxidation)が進行する側の活量を aOx 、還元反応(Reduction)が進行する側の活量を aRed とすると、反応比 \(Q\) は以下の式で求めることができます。
$$ Q = \frac{a_{Red}}{a_{Ox}} $$
上記のダニエル電池を例にすると、各活量は以下のようになるので、ここから反応比 \(Q\) を求めることができます。
$$ a_{Ox} = \frac{[Zn^{2+}]}{[Zn]} $$
$$ a_{Red} = \frac{[Cu]}{[Cu^{2+}]} $$
以上が、ネルンストの式の解説です。
>>理系課題の代行なら東大生中心スタッフ!業界最安値かつ高品質の「宿題代行Yattoku」へご依頼を
ネルンストの式の導出方法
ネルンストの式の導出には、
- その電池が行うことができる電気的仕事を求める式
- 反応ギブスエネルギーの組成依存性を表す式
の二つを理解する必要があります。
まず、その電池が行うことができる電気的仕事を求める式について解説していきます。
電池電位 \(E_{cell}\) はその電池から取り出せる電圧のことですが、電圧とは電気を流す強さを示す指標であって、どの程度の電流を流すことができるかを示すものではありません。
その電池がどの程度電流を流すことができるのか、つまりその電池がどの程度の電子を動かすほどの仕事ができるのか、は以下の式で求めることができます。
$$ -νFE_{cell} = Δ_rG $$
ここで登場する \(Δ_rG \) は、その電池から取り出せる電気的エネルギー量と簡易的に理解しておきましょう。
次に、反応ギブスエネルギーの組成依存性を表す式について解説していきます。
ある電池が理想的な稼働をすれば、その電池は標準電池電位 (E^{o}_{cell}\) を示します。しかし、現実には電池反応は理想的には進行しません。
そのような理想的な反応から実際の反応がどの程度離れているのか、つまり、取り出せる電気的エネルギーは理想状態と現実でどの程度違いがあるのか、を以下の式によって求めることができます。
$$ Δ_rG = Δ_rG^o + RTlnQ $$
| ・\(Δ_rG\):反応ギブスエネルギー ・\(Δ_rG^o\):標準反応ギブスエネルギー ・\(Q\):反応比 |
以上の二つの式を用いて、\(Δ_rG = Δ_rG^o + RTlnQ\) に \(-νFE_{cell} = Δ_rG \) を代入することでネルンストの式を導出するこができます。
ネルンストの式とは、その電池が現実に実行できる電気的な仕事を理想的に実行できる電気的な仕事を基準にして求める式ということが分かります。
ネルンストの式の実際の使い方とは?
既知のデータから未知のデータを求めることができる強力なツール
$$E_{cell} = E^{o}_{cell} \,-\,\frac{RT}{νF}lnQ $$
| ・\(E_{cell}\):電池電位 (V) ・\(E^{o}_{cell}\):標準電池電位 (V) ・\(R\):気体定数 ・\(T\):絶対温度 (K) ・\(ν\):電池反応で移動する電子の量論係数 ・\(F\):ファラデー定数 ・\(Q\):電池反応の反応比 |
ネルンストの式を利用すると、既知の値や測定データから未知の値や測定データを知ることができます。
ネルンストの式の中で、気体定数 \(R\) とファラデー定数 \(F\) は既知の定数です。一方で、電池電位 \(E_{cell}\)、標準電池電位 \(E^{o}_{cell}\)、絶対温度 \(T\)、電池反応で移動する電子の量論係数 \(ν\)、電池反応の反応比 \(Q\) は未知の値です。
この未知の値の中で、例えば、実験によって電池電位 \(E_{cell}\) 、絶対温度 \(T\)、電池反応で移動する電子の量論係数 \(ν\)、電池反応の反応比 \(Q\) が判明したとすると、ネルンストの式によって標準電池電位 \(E^{o}_{cell}\) は計算できることになります。
また、大学の課題などの問題分の中で、電池電位 \(E_{cell}\)、標準電池電位 \(E^{o}_{cell}\)、絶対温度 \(T\)、電池反応で移動する電子の量論係数 \(ν\) が与えられるとすると、ネルンストの式によって電池反応の反応比 \(Q\) を求めることができます。
このように、ネルンストの式は直接測定せずとも電池反応において重要となるこれらの値の一部を計算によって求めることができます。
>>理系課題の代行なら東大生中心スタッフ!業界最安値かつ高品質の「宿題代行Yattoku」へご依頼を
ネルンストの式を用いた例題
例題1:電池電位が分からない場合
| \(Zn^{2+} + 2e^- → Zn(s)\) の標準電池電位が \(E^{o}_{cell} = -0.76 V\) である。\(Zn^{2+}\) 濃度が 0.01 mol/L であるとき、電池電位 \(E_{cell}\) を求めよ。ただし、温度は 25 ℃である。 |
《解説》
ネルンストの式 \(E_{cell} = E^{o}_{cell} \,-\,\frac{RT}{νF}lnQ\) のうち、電池反応で移動する電子の量論係数 \(ν\) と反応比 \(Q\) が不明であるので、まずはこれらを求めます。
電池反応で移動する電子の量論係数 \(ν\) は、\(Zn^{2+} + 2e^- → Zn\) より電子が 2 個移動しているので、\(ν = 2\) です。
反応比 \(Q\) は、酸化反応(Oxidation)が進行する側は右辺の \(Zn(s)\)、還元反応(Reduction)が進行する側は左辺の \(Zn^{2+}\) です。また、溶液における溶質の活量は濃度であり、固体の活量は1とみなせます。(活量係数を考える必要がある場合はこの限りではありませんが、活量は概ねこのように考えてよいです。)
従って、反応比 \(Q\) は以下のように求めることができます。
$$Q = \frac{a_{Red}}{a_{Ox}} = \frac{[Zn^{2+}]}{1} = 0.01$$
以上より求めた値を用いると、電池電位 \(E_{cell}\) は以下のように求めることができます。
$$ E_{cell} = E^{o}_{cell} \,-\,\frac{RT}{νF}lnQ = -0.76\,-\,\frac{8.31×298}{2×96500}ln(0.01)=-0.701V$$
例題2:標準電池電位が分からないとき
| \(A^++e^- → A(s)\) の電池電位 \(E_{cell}\) は、25 ℃、\(A^+\) の濃度が 0.02 mol/L のとき、\(E_{cell} = -1.50\) であった。この反応の標準電池電位 \(E^{o}_{cell}\) を求めよ。 |
《解説》
ネルンストの式を変形して、\(E^{o}_{cell}=E_{cell} \,+\,\frac{RT}{νF}lnQ\) から求めます。
例題1と同様に考えると、電池反応で移動する電子の量論係数 \(ν\) は \(ν = 1\)、反応比 \(Q\) は \(Q = [A^+]\) であるので、標準電池電位 \(E^{o}_{cell}\) は以下のように求めることができます。
$$ E^{o}_{cell}=E_{cell} \,+\,\frac{RT}{νF}lnQ = -1.50 \,+\,\frac{8.31×298}{1×96500}ln(0.02) = -1.60 V$$
例題3:反応比(濃度)が分からないとき
| \(B^{+} + e^- → B(s)\) の標準電池電位は +0.60 V である。25 ℃において電池電位が +0.582 V の時、この反応式の反応比および\(B^{2+}\) の濃度を求めよ。 |
《解説》
ネルンストの式を変形して、\(Q = exp(\frac{νF}{RT}(E^{o}\,_\,{cell}-E_{cell})\)から求めます。
上記変形式に各条件を代入すると、反応比 \(Q\) は以下のように求めることができます。
$$ Q = exp(\frac{νF}{RT}(E^{o}\,_\,{cell}-E_{cell}) = exp(\frac{1×96500}{8.31×298}(0.60-0.582) = 2.014$$
また、この反応における反応比は \(Q = [B^+]\) であるので、\(B^{2+}\) の濃度は 2.014 mol/L と求めることができます。
まとめ
ネルンストの式は以下のような形をしており、電池電位 \(E_{cell}\)、標準電池電位 \(E^{o}_{cell}\)、反応比 \(Q\)および電池反応で移動する電子の量論係数 \(ν\) のいずれかの値が分かれば残りの値も算出することができるという強力な公式です。
$$E_{cell} = E^{o}_{cell} \,-\,\frac{RT}{νF}lnQ $$
この式の形を覚えることは勿論、この式を自力で導出することができればより理解度は深まりますし、他の分野でも役に立つ考え方を身に着けることができます。
一方で、ネルンストの式を覚えていることと実際に使いこなせることは別物だったりします。
例えば、実験で得られたデータをどのようにネルンストの式に当てはめていくのか、そもそもネルンストの式が使えるのか、ネルンストの式以外の知識を組み合わせていく必要があるのか、など応用するにはネルンストの式以外にも知識が必要になってきます。
ネルンストの式を目的として学ぶことはできても、何を知る必要があるのかがそもそも分からなければ課題をやろうにもできません。そんなときは、知っていそうな友人に訪ねてみたり、宿題代行サービスを裏技的に利用することがおすすめです。

