大学の物理化学(特に熱力学)では『状態関数』という新たな概念が登場します。さらにその状態関数には、示量性状態関数と示強性状態関数のように分類されます。
初心者にとっては状態関数は聞きなれない単語ですし、そこに示量性や示強性が加わると余計に分からなくなると思います。
本記事では、
- 状態関数とは何か?
- 示量性状態関数、示強性状態関数とは何か?
- それらの簡単な見分け方とは?
について分かりやすく解説していきます。
状態関数とは?
その系の状態から決まる性質のこと
状態関数とは、その系が置かれている状態にのみ依存するパラメータのことです。
どういうことかと言うと、状態関数はその系のパラメータを使って算出可能であるものということです。
例えば、理想気体の状態関数 \(PV = nRT\) を変形して、\(P = \frac{nRT}{V}\) とします。この時、その気体の物質量 \(n\)、温度 \(T\)、体積 \(V\) といったパラメータが決まれば、自ずと圧力 \(P\) も決定します。
すなわち、圧力 \(P\) はその系が置かれている状態によって決まる性質(=状態関数)ということです。
また、\(P = \frac{nRT}{V}\) をみると物質量 \(n\)、温度 \(T\)、体積 \(V\) は変数として圧力 \(P\) をかえす関数となっています。このことからも、状態『関数』と称されます。
状態関数には、例えば、内部エネルギー \(U\)、エンタルピー \(H\)、エントロピー \(S\)、圧力 \(P\)、体積 \(V\)、物質量 \(n\)などがあります。
>>理系科目の課題代行・レポート代行なら業界最安値の「宿題代行Yattoku」へご依頼ください!
示量性状態関数と示強性状態関数の違いとは?
状態関数には示量性と示強性の種類がある
話は変わりますが、数学的には関数と関数は足し算することが可能です。連立方程式などで実際に関数と関数を足し合わせたことがあると思います。
しかしながら、状態関数には関数という言葉がありますが、状態関数と状態関数を足し算ができる場合と足し算ができない場合があります。
これは、状態関数が系の現実での物理的性質を表すものであるため、状態関数と状態関数を足し算しても現実の現象を上手く表現できないことがあるためです。
示量性状態関数とは足し算可能な状態関数
『示量性』とは、足し算が可能であるという性質であり、『示量性状態関数』とは足し算な可能な状態関数のことを指します。
例えば、体積 \(V_1\) の液体 A と体積 \(V_2\) の液体 B を混合すると、混合した液体 C の体積 \(V\) は \(V_1 + V_2\) となります(下記図参照)。コップに水を注ぐ場合を想像すれば、コップの中の水の体積は入れた水の分だけ増えます(=足し算される)。
すなわち、体積 \(V\) は足し算が可能な状態関数ということです。
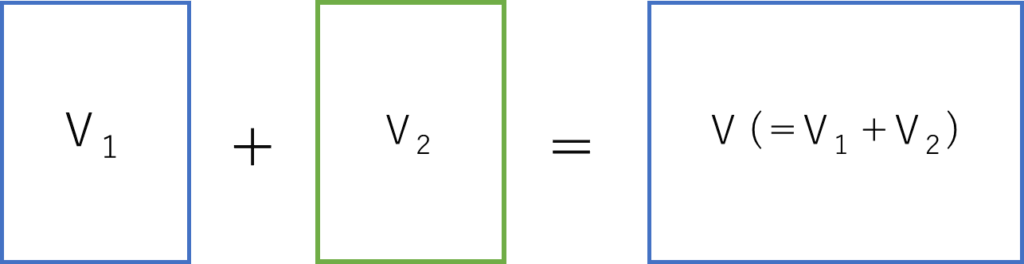
示量性状態関数としては、体積 \(V\)、内部エネルギー \(U\)、エンタルピー \(H\)、エントロピー \(S\) などがあります。
内部エネルギー \(U\)、エンタルピー \(H\) は系のエネルギーの指標であり、見ている世界は原子や分子の持つエネルギーの総計、つまりは量です。
例えば、内部エネルギーが \(U_1\) である気体 A と、内部エネルギーが \(U_2\) である気体 B を混合した場合、混合気体 C には内部エネルギーが \(U_1\) である気体 A の分子と、内部エネルギーが \(U_2\) である気体 B の分子との両方が存在することになります。つまり、混合気体 C の内部エネルギー \(U\) は \(U_1 + U_2\) ということになります。
>>理系科目の課題代行・レポート代行なら業界最安値の「宿題代行Yattoku」へご依頼ください!
示強性状態関数は足し算ができない状態関数
『示強性状態関数』は、示量性状態関数とは異なり足し算ができない状態関数です。
例えば、0℃の水と50℃の水を同じ量だけ混合すると、混合した水の温度は何度になるでしょうか。足し算した場合は混合した水の温度は0+50=50より50℃となりそうですが、実際には25℃くらいになります。
示強性状態関数としては、圧力 \(P\)、温度 \(T\)、密度、濃度などがあります。
示量性状態関数と示強性状態関数の簡単な見分け方を解説
示量性状態関数と示強性状態関数の見分け方としては、その系を『大きい・小さい』と評価するか、『高い・低い』で評価するかによって簡単に見分けることができます。
例えば、体積 \(V\) の場合には体積が『大きい』と言いますし、量としてのエネルギーの場合にはエネルギーが『大きい』と言います。そして、体積 \(V\)やエネルギーの量を表す内部エネルギー \(U\) やエンタルピー \(H\) は示量性状態関数であり、足し算が可能な状態関数です。
つまり、その系のあるパラメータを『大きい・小さい』と評価するものは示量性状態関数と判断できます。
また、温度 \(T\) の場合には温度が『高い』と言いますし、圧力 \(P\) の場合には圧力が『高い』と言います。そして、温度 \(T\) や圧力 \(P\) は示強性状態関数であり、足し算ができない状態関数です。
つまり、その系のあるパラメータを『高い・小さい』と評価するものは示強性状態関数と判断できます。
このように、『大きい・小さい』又は『高い・低い』のどちらかを使うかによって比較的簡単に示量性状態関数か示強性状態関数かを見分けることができます。
まとめ:示量性状態関数と示強性状態関数はイメージで理解しよう
示量性状態関数と示強性状態関数の性質とその見分け方は以下の表のようにまとめることができます。
| 性質 | 見分け方 | |
| 示量性状態関数 | 足し算が可能 | ~が『大きい・小さい』と言うもの |
| 示強性状態関数 | 足し算ができない | ~が『高い・低い』と言うもの |
状態関数を一つずつ覚えて、一つずつ示量性状態関数か示強性状態関数かを覚えることも有効ですが、より応用を効かせるためには示量性状態関数と示強性状態関数とをイメージで理解することが重要です。
しかし、イメージで理解するためには示量性状態関数と示強性状態関数とを抽象的に、かつ理論的に理解することや、自分自身が腑に落ちるような理解をする必要がある場合があります。
状態関数やその示量性、示強性を知識として落とし込みきれていないと、自力で大学のレポートや課題をやろうとしても分からずにやりきれないという状況が出てくると思います。そのような時は、宿題代行Yattokuのような代行サービスを利用することで、確実に単位を取れるレポートを仕上げることができます。

