大学の物理化学の分野で登場する”化学ポテンシャル”という単語。
教科書やインターネットで調べても、定義に沿った説明や導出の方法は書いてあっても、結局のところ”化学ポテンシャル”とは物質のどのような性質を表しているのか、については納得に及ばないことがよくあります。
筆者自身も大学時代、”化学ポテンシャル”について非常に頭を悩ませました。
そのような経験も踏まえて、本記事では、例示や例題を駆使しながら”化学ポテンシャル”とはどういったものなのかを分かりやすく解説していきます。
>>理系大学の課題代行なら東大生を中心とした精鋭スタッフかつ業界最安値の「宿題代行Yattoku」へご依頼を
化学ポテンシャルとは結局のところ何なのか?
化学ポテンシャルとは『位置エネルギーの化学版』
高校物理では位置エネルギーというものが登場しました。位置エネルギーとは、ある位置にある物質が持つ潜在的なエネルギーのことです。
例えば、地上から 1 m の高さでりんごを手に持っているとします。当然、りんごを持っている間はそのりんごは動いていないので運動エネルギーはゼロです。
ここで、りんごを静かに手から離せば、そのりんごは下に自然と落下します。この時は、りんごは動いてるため運動エネルギーを持っているということになりますが、りんごに勢いをつけて落としたわけでもないのにどうしてりんごは動きだすのでしょうか。
それは、りんごには常に鉛直下向きに重力という力が働いているためであり、ある高さでりんごを手に持っているとき、そのりんごは下向きに動くためのエネルギーを潜在的に持っているということになります。
これが位置エネルギーであり、別名、ポテンシャルエネルギーとも言います。
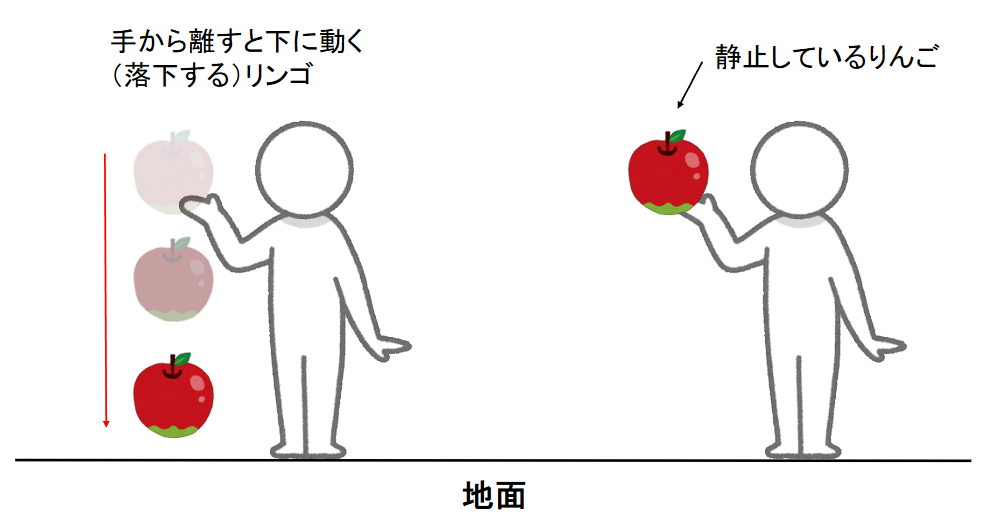
図1:位置エネルギー
物理でいう、止まっているけど潜在的には運動エネルギー(運動を引き起こす能力)を有しているという概念は、実は化学でも同じようなことが言えます。
例えば、ここに砂糖があるとします。この砂糖は目に見える大きさの結晶を形成していて、そこにあるだけは何の変化もありません。
ところが、この砂糖を水の中に入れると、自然と砂糖がバラバラになって水の中に分散します。この時、砂糖そのものに対しては何もしてないはずですが、砂糖は勝手にバラバラになります。
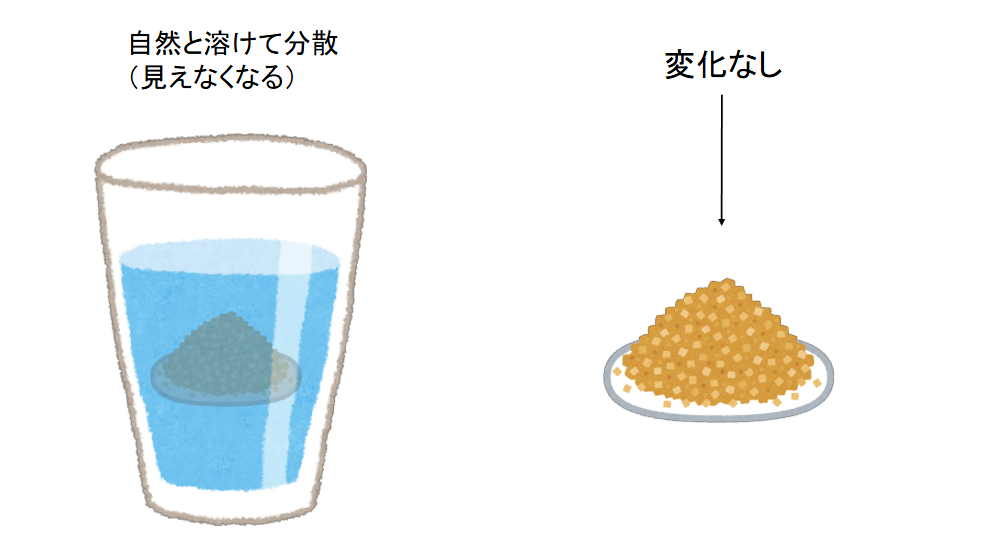
図2:砂糖を放置した場合と水に入れた場合
すなわち、砂糖は水の中に入れると自然とバラバラになって水の中に分散する潜在的な能力を持っていることになります。
他にも、塩酸と水酸化ナトリウム水溶液を混ぜると中和反応が生じる、煙は自然と空気中に拡散して見えなくなる、ルシャトリエの法則に沿った経験則的な平衡移動など、化学においても物質そのもに対しては何もしていないのに反応や拡散などが自然と生じる場合があります。
これもすべて、物質が潜在的な能力(=化学ポテンシャル)を有しているために生じることと解釈できます。
このように、化学ポテンシャルとはある状況において、化学反応やその他化学的現象を引き起こすための潜在的な能力のことであると理解できます。
>>理系大学の課題代行なら東大生を中心とした精鋭スタッフかつ業界最安値の「宿題代行Yattoku」へご依頼を
ギブスエネルギーから理解する化学ポテンシャル
混合物におけるギブスエネルギー
ギブスエネルギー \(G\) とは、端的に言えばその系や物質が自発変化を引き起こすかどうかの指標です。そして、系や物質はギブスエネルギーが低い方向へ変化しようとする傾向があります。
例えば、A という物質が B という物質に変化するときのギブスエネルギーが負であれば、その反応は概ね進行します。一方で、正であればその反応はほとんど進行しません。
また、例えば、物質 A と物質 B からなる混合物の場合でもギブスエネルギー \(G\) の正負で自発変化が生じるか否かを判断することができ、以下の式で表せます。
化学ポテンシャル \(μ\) には次のような関係があります。
$$ G = n_AG_A + n_BG_B $$
| ・\(n_A, n_B\) は物質 A, B それぞれのモル分率、 ・\(G_A, G_B\) は物質 A, B それぞれのモルギブスエネルギー |
ここに物質 A と物質 B からなる混合物があるとします。この混合物のギブスエネルギー \(G\) は上式によって得られます。
式中に登場する部分モルギブスエネルギー \(G_A, G_B\) とは、全体のギブスエネルギーのうち各物質が占めるギブスエネルギーのことです。
物質の反応は微視的な視点で見ると、原子や分子同士の反応です。例えば、水が水蒸気へと蒸発する場合も、結局のところ水分子一つ一つの状態が変化する反応です。
そのため、ある分子を取り囲む状況によってはある反応が自発的に生じやすいか、生じにくいかが変わってきます。
下記図を参照すると、純粋な水におけるある水分子の周囲は同じ水分子に囲まれていますが、食塩水におけるある水分子はナトリウムイオンおよび塩化物イオンに囲まれています。
水分子-水分子の相互作用と、水分子-ナトリウムイオンおよび塩化物イオンの相互作用は異なるため、純粋な水と食塩水とではある水分子の動きやすさや他分子との接触(反応)にも違いが生じてきます。
すなわち、ある分子を取り囲む状況によってはある分子の反応性(反応を引き起こす潜在的な能力)も変化します。
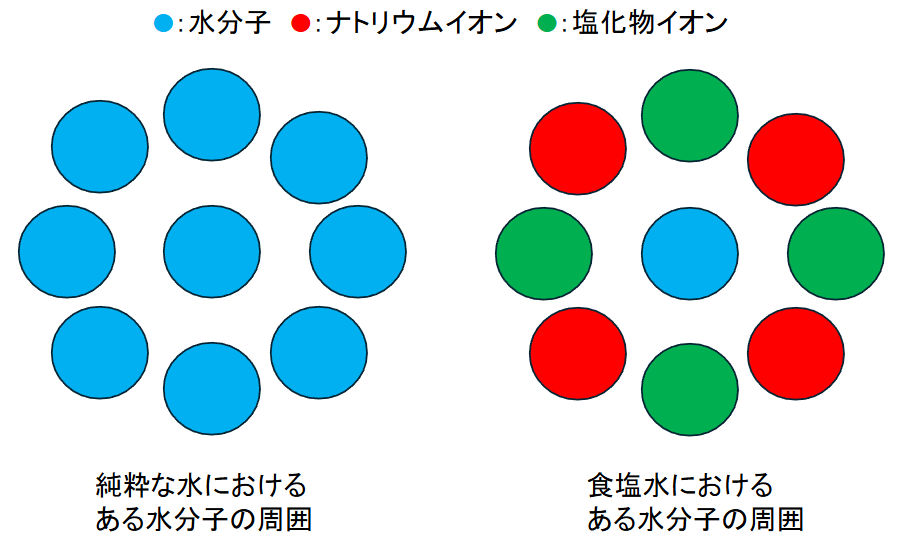
図3:純粋な水と食塩水における水分子を取り囲む環境の違い
また、各物質が全体に占める割合もある分子を取り囲む環境に影響するため重要です。
例えば、水に対して 1 % の食塩を加えた場合と、水に対して 50 % の食塩を加えた場合とでは、食塩水中の食塩分子(正確にはナトリウムイオンや塩化物イオン)の数が異なってくるため、水分子を取り囲む食塩分子(正確にはナトリウムイオンや塩化物イオン)の数も異なります。
このように、混合物においては各物質の種類や割合によって、各物質が反応を引き起こす潜在的な能力に変化が生じ、部分モルギブスエネルギーはこのことを表現しています。
>>理系大学の課題代行なら東大生を中心とした精鋭スタッフかつ業界最安値の「宿題代行Yattoku」へご依頼を
部分モルギブスエネルギーと化学ポテンシャル
上式をさらに変形すると以下のようになります。
$$ G = n_AG_A + n_BG_B = n_Aμ_A + n_Bμ_B $$
| ・\(n_A, n_B\) は物質 A, B それぞれのモル分率、 ・\(G_A, G_B\) は物質 A, B それぞれの部分モルギブスエネルギー ・\(μ_A, μ_B\) は物質A, B それぞれの化学ポテンシャル |
この式が示すことは部分モルギブスエネルギーと化学ポテンシャルは等価ということであり、前述した部分モルギブスエネルギーの簡易な説明がそのまま当てはまります。
すなわち、化学ポテンシャルは混合物においては各物質の種類や割合を考慮した、各物質が反応を引き起こす潜在的な能力ということであり、最初の化学ポテンシャルの表現に帰着します。
式からみる化学ポテンシャル
化学ポテンシャルの一般式
化学ポテンシャルは以下のような式で定量的に表現することができます。
$$ μ = μ^o + RTlna $$
| ・\(μ\) :化学ポテンシャル ・\(μ^o\) :標準化学ポテンシャル ・\(a\) :活量 |
標準化学ポテンシャル \(μ^o\) とは圧力が 1 bar の時の化学ポテンシャルのことであり、活量 \(a\) はある成分の実効的な濃度のことです。
例えば、A という物質と B という物質が反応して 物質 C が生成する反応(A + B → C)においては、物質 A の分子と物質 B の分子が接触することで反応が生じて物質 C が生成します。一方で、物質 A の分子と物質 B の分子が接触しなければ何の反応も起きません。
この場合、物質 A が大量に存在し、物質 B が少量しかない場合、物質 A の分子は同じ物質 A の分子と接触する機会が多くなりますし、逆に物質 B は物質 A の分子と接触する機会が多くなります。
すなわち、物質の濃度によって反応に寄与する度合いが異なり、これを活量といいます。
完全気体や完全希薄溶液における活量 \(a\) は以下のように求めることができます。
| 物質 | 活量 \(a\) |
| 固体 | 1 |
| 液体 | 1 |
| 気体 | \(p\)/\(p^o\) |
| 溶質 | \(c\)/\(c^o\) |
| 溶媒 | \(x\) |
※\(p^o = 1 bar、c^o = 1 mol/dm^3\)
例題1
| 1 bar, 298 K。N₂ 0.7 mol と O₂ 0.3 mol を混合して、全圧 1 bar の理想混合気体にする。各成分の化学ポテンシャルの変化量 Δμᵢ(純物質=1 bar を基準)を求めよ。 |
《方針》
N2 と O2 の化学ポテンシャルを求めて、\( G = n_AG_A + n_BG_B\) に代入する。
《解法》
N2 と O2 それぞれの分圧は、1 bar × (モル分率) で求められるので、
- N2 の分圧:\(P_1 = 1 bar × \frac{0.7}{0.7+0.3} = 0.7 \)
- O2 の分圧:\(P_1 = 1 bar × \frac{0.3}{0.7+0.3} = 0.3 \)
圧力が 1 bar の時の各成分の化学ポテンシャル(標準化学ポテンシャル)を基準に、各成分が上記分圧時の化学ポテンシャルの差を求める。
$$ μ_1 = (圧力が分圧時の化学ポテンシャル)ー(圧力が 1 bar の時の化学ポテンシャル)$$
$$ = μ^o + RT ln 0.7 ー (μ^o + RT ln 1)= RT ln 0.7 = −884 J mol⁻¹$$
O2 も同様にして求めると、\(μ_2 = −2984 J mol⁻¹\)
《解説》
化学標準ポテンシャル \(μ^o\) が分からなくても、上記の方法で化学ポテンシャルを求めることができます。
>>理系大学の課題代行なら東大生を中心とした精鋭スタッフかつ業界最安値の「宿題代行Yattoku」へご依頼を
例題2
| 上記の混合気体のギブスエネルギー \(G\) を求めよ。 |
《方針》
(部分モルギブスエネルギー)=(化学ポテンシャル)であるので、例題1の結果を用いて計算する。
《解法》
- N2 の化学ポテンシャル:−884 J mol⁻¹
- O2 の化学ポテンシャル:−2984 J mol⁻¹
したがって、
$$ G = 0.7 × (−884) + 0.3 × (−2984) = -1514 J mol⁻¹$$
と求めることができます。
まとめ
化学ポテンシャルとは、端的に言えば化学反応や現象を引き起こすための潜在的な能力です。
イメージ的にはこのように理解できますが、理論的に使いこなそうとするとまだまだこんなものでは足りません。
化学ポテンシャルを使いこなせないうちは大学の課題などをこなすのが非常に困難となると思います。そんな時は、宿題代行Yattoku といった代行サービスを利用することもおすすめします。

